A hyperbolic spiral is a type of spiral familiar from the view up a spiral staircase[1] and the starting arrangement of certain footraces,[2] and used to model spiral galaxies[3][4] and architectural volutes.[5] Its pitch angle increases with distance from its center, unlike the constant angles of logarithmic spirals or decreasing angles of Archimedean spirals. As this curve widens, it approaches an asymptotic line.
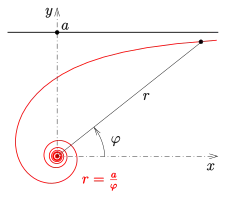
As a plane curve, a hyperbolic spiral can be described in polar coordinates by the equation
for an arbitrary choice of the scale factor . Because of the reciprocal relation between its two coordinates it is also called a reciprocal spiral.[6] The same relation between Cartesian coordinates would describe a hyperbola, and the hyperbolic spiral was first discovered by applying the equation of a hyperbola to polar coordinates.[7] Hyperbolic spirals can also be generated as the inverse curves of Archimedean spirals,[8][9] or as the central projections of helixes.[1]
History and applications
Pierre Varignon first studied the hyperbolic spiral in 1704,[10][11] as an example of the polar curve obtained from another curve (in this case the hyperbola) by reinterpreting the Cartesian coordinates of points on the given curve as polar coordinates of points on the polar curve. Varignon and later James Clerk Maxwell were interested in the roulettes obtained by tracing a point on this curve as it rolls along another curve; for instance, when a hyperbolic spiral rolls along a straight line, its center traces out a tractrix.[7]
Johann Bernoulli and Roger Cotes also worked on this curve, in connection with Isaac Newton's discovery that bodies moving under an inverse-square law, such as the one in Newton's law of universal gravitation, follow conic section trajectories. Newton, Bernoulli, and Cotes were interested in reversing this implication, and determining the form of gravitational law required to produce a trajectory of a given form. Newton showed that a logarithmic spiral trajectory required an inverse-cube law, Bernoulli extended this to the hyperbolic spiral, and Cotes found a family of spirals, the Cotes's spirals, including the logarithmic and hyperbolic spirals, that all required an inverse-cube law.[12]
For a hyperbolic spiral with equation , a circular arc centered at the origin, continuing clockwise for length from any of its points, will end on the -axis.[8] Because of this equal-length property, the starting marks of 200m and 400m footraces are placed in staggered positions along a hyperbolic spiral. This ensures that the runners, restricted to their concentric lanes, all have equal-length paths to the finish line. For longer races where runners move to the inside lane after the start, a different spiral (the involute of a circle) is used instead.[2]
The increasing pitch angle of the hyperbolic spiral, as a function of distance from its center, has led to the use of these spirals to model the shapes of some spiral galaxies, which in some cases have a similarly increasing pitch angle. However, this model does not provide a good fit to the shapes of all spiral galaxies.[3][4] In architecture, it has been suggested that hyperbolic spirals are a good match for the design of volutes from columns of the Corinthian order.[5]
Along with the Archimedean and logarithmic spiral, the hyperbolic spiral has been used in psychological experiments on the perception of rotation.[14]
Constructions
Coordinate equations
The hyperbolic spiral has the polar equation
for polar coordinates and scale coefficient . It can be represented in Cartesian coordinates by applying the standard polar-to-Cartesian conversions and , obtaining a parametric equation for the Cartesian coordinates of this curve that treats as a parameter rather than as a coordinate:[15]
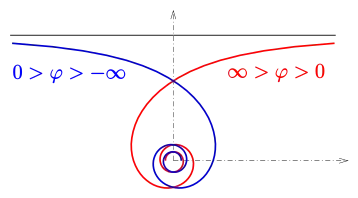
Relaxing the constraint that to and using the same equations produces a reflected copy of the spiral, and some sources treat these two copies as branches of a single curve.[9][16]
The hyperbolic spiral is a transcendental curve, meaning that it cannot be defined from a polynomial equation of its Cartesian coordinates.[15] However, one can obtain a trigonometric equation in these coordinates by starting with its polar defining equation in the form and replacing its variables according to the Cartesian-to-polar conversions and , giving:[17]
Inversion
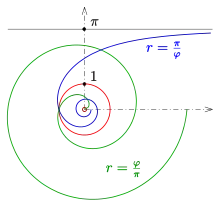
Circle inversion through the unit circle is a transformation of the plane that, in polar coordinates, maps the point (excluding the origin) to and vice versa.[18] The image of an Archimedean spiral under this transformation (its inverse curve) is the hyperbolic spiral with equation .[11]
Central projection of a helix

The central projection of a helix onto a plane perpendicular to the axis of the helix describes the view that one would see of the guardrail of a spiral staircase, looking up or down from a viewpoint on the axis of the staircase.[1] To model this projection mathematically, consider the central projection from point onto the image plane . This will map a point to the point .[19]
The image under this projection of the helix with parametric representation
is the curve
with the polar equation
which describes a hyperbolic spiral.[19]
Properties
Asymptotes
The hyperbolic spiral approaches the origin as an asymptotic point.[17] Because
the curve has an asymptotic line with equation .[15]
Pitch angle

From vector calculus in polar coordinates one gets the formula for the pitch angle between the tangent of any curve and the tangent of its corresponding polar circle.[20] For the hyperbolic spiral the pitch angle is[14]
Curvature
The curvature of any curve with polar equation is[21]
From the equation and its derivatives and one gets the curvature of a hyperbolic spiral:[22]
Arc length
The length of the arc of a hyperbolic spiral between the points and can be calculated by the integral:[15]
Sector area
The area of a sector (see diagram above) of a hyperbolic spiral with equation is:[15]
That is, the area is proportional to the difference in radii, with constant of proportionality .[15]
References
- 1 2 3 Hammer, Øyvind (2016), "15: The case of the staircase", The Perfect Shape: Spiral Stories, Springer International Publishing, pp. 65–68, doi:10.1007/978-3-319-47373-4_15
- 1 2 Haines, C. R. (December 1977), "Old curves in a new setting", The Mathematical Gazette, 61 (418): 262–266, doi:10.2307/3617399, JSTOR 3617399
- 1 2 Kennicutt, R. C. Jr. (December 1981), "The shapes of spiral arms along the Hubble sequence", The Astronomical Journal, American Astronomical Society, 86: 1847, Bibcode:1981AJ.....86.1847K, doi:10.1086/113064
- 1 2 Savchenko, S. S.; Reshetnikov, V. P. (September 2013), "Pitch angle variations in spiral galaxies", Monthly Notices of the Royal Astronomical Society, 436 (2): 1074–1083, doi:10.1093/mnras/stt1627
- 1 2 Nicholson, Peter (1825), A Popular Course of Pure and Mixed Mathematics for the Use of Schools and Students, G. B. Whittaker, p. 436
- ↑ Waud, Samuel Wilkes (1835), A Treatise on Algebraical Geometry, Baldwin and Cradock, p. 194
- 1 2 Maxwell, James Clerk (1849), "XXXV.—On the theory of rolling curves", Transactions of the Royal Society of Edinburgh, 16 (5): 519–540, doi:10.1017/s008045680002247x
- 1 2 Bowser, Edward Albert (1882), "The reciprocal or hyperbolic spiral", An Elementary Treatise on Analytic Geometry: Embracing Plane Geometry and an Introduction to Geometry of Three Dimensions (4th ed.), D. Van Nostrand, p. 232
- 1 2 Drábek, Karel (1994), "Plane curves and constructions", in Rektorys, Karel (ed.), Survey of Applicable Mathematics, Mathematics and Its Applications, vol. 280–281, Springer Netherlands, pp. 112–166, doi:10.1007/978-94-015-8308-4_4, ISBN 9789401583084; see p. 138
- ↑ Varignon, Pierre (1704), "Nouvelle formation de Spirales – exemple II", Mémoires de l’Académie des sciences de l’Institut de France: 94–103
- 1 2 "Curves: Hyperbolic Spiral", MacTutor History of Mathematics Archive, University of St Andrews
- ↑ Hammer (2016), pp. 119–120.
- ↑ Ringermacher, Harry I.; Mead, Lawrence R. (July 2009), "A new formula describing the scaffold structure of spiral galaxies", Monthly Notices of the Royal Astronomical Society, 397 (1): 164–171, arXiv:0908.0892, Bibcode:2009MNRAS.397..164R, doi:10.1111/j.1365-2966.2009.14950.x
- 1 2 Scott, Thomas R.; Noland, J. H. (1965), "Some stimulus dimensions of rotating spirals", Psychological Review, 72 (5): 344–357, doi:10.1037/h0022204, ProQuest 614277135
- 1 2 3 4 5 6 Polezhaev, Andrey (2019), "Spirals, their types and peculiarities", in Tsuji, Kinko; Müller, Stefan C. (eds.), Spirals and Vortices: In Culture, Nature, and Science, The Frontiers Collection, Springer International Publishing, pp. 91–112, doi:10.1007/978-3-030-05798-5_4, ISBN 9783030057985; see especially Section 2.2, Hyperbolic spiral, p. 96
- ↑ Morris, Christopher G., ed. (1992), "Hyperbolic spiral", Academic Press Dictionary of Science and Technology, Academic Press, p. 1068
- 1 2 Shikin, Eugene V. (2014), "Hyperbolic spiral (reciprocal spiral)", Handbook and Atlas of Curves, CRC Press, pp. 222–223, ISBN 9781498710671
- ↑ Mumford, David; Series, Caroline; Wright, David (2002), "Inversions and the Riemann sphere", Indra's Pearls: The Vision of Felix Klein, Cambridge University Press, p. 54, ISBN 9781107717190, MR 3558870
- 1 2 Loria, Gino; Roever, W. H. (February 1919), "On certain constructions of descriptive geometry", The American Mathematical Monthly, 26 (2): 45–53, doi:10.1080/00029890.1919.11998485, JSTOR 2973138; for the central projection of a helix, see p. 51
- ↑ Kepr, Bořivoj (1994), "Differential geometry", in Rektorys, Karel (ed.), Survey of Applicable Mathematics, Mathematics and Its Applications, vol. 280–281, Springer Netherlands, pp. 260–335, doi:10.1007/978-94-015-8308-4_9, ISBN 9789401583084. For an equivalent formula for the direction angle (the complementary angle to the pitch angle) see Section 9.9, Theorem 1, p. 300
- ↑ Rutter, J.W. (2018), "Theorem 7.11", Geometry of Curves, CRC Press, p. 143, ISBN 9781482285673
- ↑ Ganguli, Surendramohan (1926), "289: The hyperbolic spiral", The Theory of Plane Curves, vol. II (2nd ed.), University of Calcutta, pp. 364–365