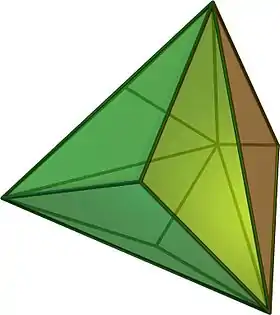
| Truncated triakis tetrahedron | |
|---|---|
 | |
| Type | Near-miss Johnson solid |
| Faces | 4 hexagons 12 irregular pentagons |
| Edges | 42 |
| Vertices | 28 |
| Vertex configuration | 4 (5.5.5) 24 (5.5.6) |
| Conway notation | t6kT = dk6tT |
| Symmetry group | Td |
| Dual polyhedron | Hexakis truncated tetrahedron |
| Properties | convex |
| Net | |
 | |
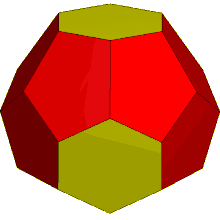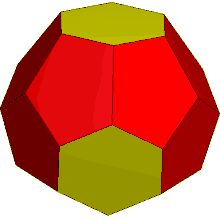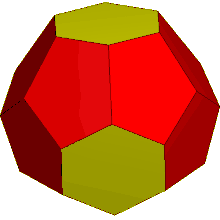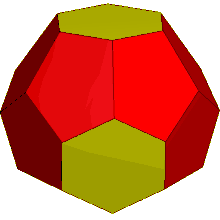
In geometry, the truncated triakis tetrahedron, or more precisely an order-6 truncated triakis tetrahedron, is a convex polyhedron with 16 faces: 4 sets of 3 pentagons arranged in a tetrahedral arrangement, with 4 hexagons in the gaps.
Construction
It is constructed from a triakis tetrahedron by truncating the order-6 vertices. This creates 4 regular hexagon faces, and leaves 12 mirror-symmetric pentagons.
A topologically similar equilateral polyhedron can be constructed by using 12 regular pentagons with 4 equilateral but nonplanar hexagons, each vertex with internal angles alternating between 108 and 132 degrees.
Topologically, as a near-miss Johnson solid, the four hexagons corresponding to the face planes of a tetrahedron are triambi, with equal edges but alternating angles, while the pentagons only have reflection symmetry.
Full truncation
If all of a triakis tetrahedron's vertices, of both kinds, are truncated, the resulting solid is an irregular icosahedron, whose dual is a trihexakis truncated tetrahedron.
Truncation of only the 3-valence vertices yields the order-3 truncated triakis tetrahedron, which looks like a tetrahedron with each face raised by a low triangular frustum. The dual to that truncation will be the triakis truncated tetrahedron.
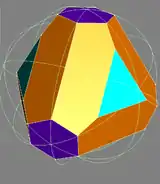
Hexakis truncated tetrahedron
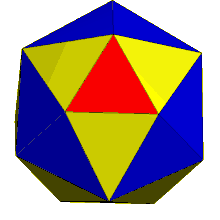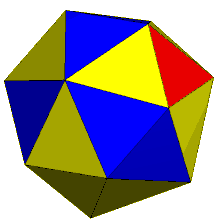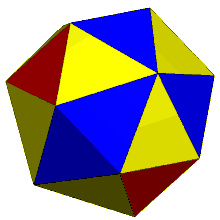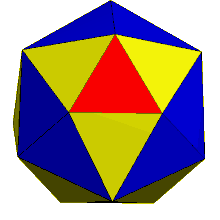
The dual of the order-6 Truncated triakis tetrahedron is called a hexakis truncated tetrahedron. It is constructed by a truncated tetrahedron with hexagonal pyramids augmented. If all of the triangles are made regular, the polyhedron becomes a failed Johnson solid, with coplanar triangles in a truncated tetrahedron volume.
 truncated tetrahedron |
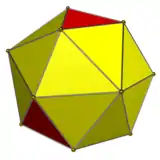 Hexakis truncated tetrahedron |
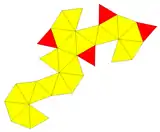 Net |
See also
External links
- Johnson Solid Near Misses: Number 22
- George Hart's Polyhedron generator - "t6kT" (Conway polyhedron notation)