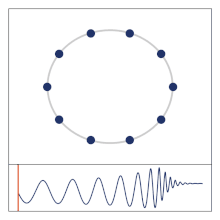
As the gravitational wave propagates perpendicular to the plane of inertial masses (in free fall), it is displaced by an amount proportional to the gravitational wave strain. After the gravitational wave has passed, the masses are permanently displaced, due to the gravitational memory effect.[1]

Gravitational memory effects, also known as gravitational-wave memory effects are predicted persistent changes in the relative position of pairs of masses in space due to the passing of a gravitational wave.[2] Detection of gravitational memory effects has been suggested as a way of validating Einstein's Theory of General Relativity.[3]

There are two kinds of predicted gravitational memory effect: a linear phenomenon, first proposed in 1974 by Russian scientists; and a non-linear phenomenon known as the nonlinear memory effect, which was first proposed in the 1990s.[4][5]

Research on the predicted phenomena has been carried out by Ya. B. Zel'dovich and A. G. Polnarev,[2][6] V. B. Braginsky and L. P. Grishchuk,[2][7] and Demetrios Christodoulou.[8]

In 2014 Andrew Strominger and Alexander Zhiboedov showed that the formula related to the memory effect is the Fourier transform in time of Weinberg's soft graviton theorem.[9]

In 2016, a new type of memory effect induced by gravitational waves moving along opposite circular trajectories was proposed, caused by the angular momentum of the waves themselves and therefore termed gravitational spin memory. As in the previous case, this memory also turns out to be a Fourier transform in time. In this case of the graviton theorem expanded to the subleading term.[10][11]

Detection

The effect should, in theory, be detectable by recording changes in the distance between pairs of free-falling objects in spacetime before and after the passage of gravitational waves. The proposed LISA detector is expected to detect the memory effect easily. In contrast, detection with the existing LIGO is complicated by two factors. First, LIGO detection targets a higher frequency range than is desirable for detection of memory effects. Secondly, LIGO is not in free-fall, and its parts will drift back to their equilibrium position following the passage of the gravitational waves. However, as thousands of events from LIGO and similar earth-based detectors are recorded and statistically analyzed over the course of several years, the cumulative data may be sufficient to confirm the existence of the gravitational memory effect.[12]

References

  1. ↑ Mitman, Keefe (1991-09-16). "Computation of displacement and spin gravitational memory in numerical relativity". Physical Review D. 102 (10): 104007–104027. doi:10.1103/PhysRevD.102.104007. S2CID 226245938.
  2. 1 2 3 Gibbons, G. W. (July 4, 2017). "The gravitational memory effect: what it is and why Stephen and I did not discover it" (PDF).
  3. ↑ ARC Centre of Excellence for Gravitational Wave Discovery (February 4, 2020). "Astronomers search for gravitational-wave memory". phys.org. Retrieved 2020-07-31.
  4. ↑ Favata, Marc. "Gravitational-wave memory: an overview" (PDF).
  5. ↑ Choi, Charles (12 October 2016). "Gravitational Waves May Permanently Alter Spacetime". www.pbs.org. WGBH/Nova. Retrieved 9 December 2021.
  6. ↑ Ya. B. Zel’dovich and A. G. Polnarev, “Radiation of gravitational waves by a cluster of superdense stars,” Astron. Zh. 51, 30 (1974) [Sov. Astron. 18 17(1974)].
  7. ↑ V. B. Braginsky and L. P. Grishchuk, Kinematic resonance and the memory effect in free mass gravitational antennas, Zh. Eksp. Teor. Fiz. 89 744–750 (1985) [Sov.Phys. JETP 62, 427 (1985)].
  8. ↑ Christodoulou, Demetrios (1991-09-16). "Nonlinear nature of gravitation and gravitational-wave experiments". Physical Review Letters. 67 (12): 1486–1489. Bibcode:1991PhRvL..67.1486C. doi:10.1103/PhysRevLett.67.1486. ISSN 0031-9007. PMID 10044168.
  9. ↑ Strominger, Andrew; Zhiboedov, Alexander (2014). "Gravitational Memory, BMS Supertranslations and Soft Theorems". arXiv:1411.5745 [hep-th].
  10. ↑ The formula for the soft graviton theorem is based on a Laurent series expansion. Weinberg calculations were limited to the first term of order -1.
  11. ↑ Pasterski, Sabrina; Strominger, Andrew; Zhiboedov, Alexander (14 December 2016). "New gravitational memories". Journal of High Energy Physics. 2016 (12): 53. arXiv:1502.06120. Bibcode:2016JHEP...12..053P. doi:10.1007/JHEP12(2016)053. S2CID 256045385.
  12. ↑ McCormick, Katie (8 December 2021). "Gravitational Waves Should Permanently Distort Space-Time". Quanta Magazine. Retrieved 9 December 2021.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.